実験や測定でデータが集まったとき、習慣的にグラフを描くことがデータ分析の基本です。データの分布形状によって、用いるべき検定法が変わってしまうからです。
ゆえにデータが集まったら、どのような分布のデータなのか全体像をみるためにグラフ化しましょう。
Contents
データ分析のポイント：グラフでデータを可視化する
グラフ形状は正規分布か非正規分布なのか大別することができます。
正規分布と非正規分布
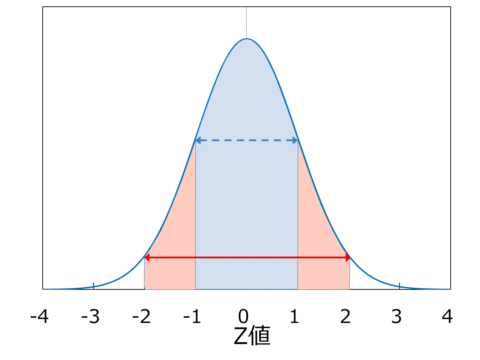
正規分布
正規分布は左右対称の釣鐘型の分布です。
グラフの横軸はＺ値と示しましたが、測定値とすればグラフ中央は平均値と等しくなります。
正規分布の特徴は全事象が起きる確率を100%としたとき、平均値から±1σ（標準偏差）離れた点までに入る確率（青部分）が68.26%、±2σ（赤部分）が95.44% ±3σが99.74%になることです。
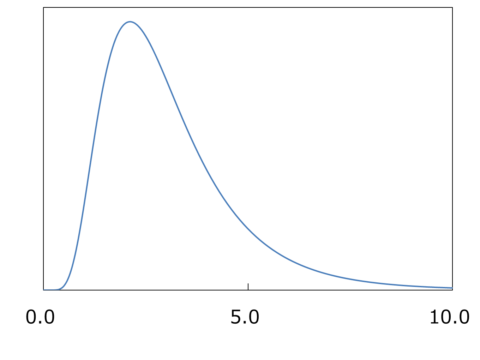
対数正規分布
対数正規分布はLog normal distributionと表現されます。どちらかの軸を対数にとると、正規分布のような形と同じ分布になります。
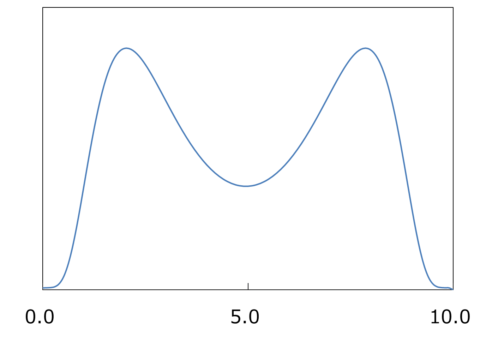
非正規分布
正規分布、対数正規分布に含まれないものを指します。下図は双極性（2峰性）分布の例です。
このグラフは対数正規分布を組み合わせてつくったもので、もし「男女」などデータをクラスター（階層）に分割することが可能であれば、正規分布にできる場合もあります。
データを数値で分析する基本統計量
グラフ化するだけでなく平均値や標準偏差などを使って、データを数値で要約するとき『基本統計量』というものがあります。基本統計量には、中心的な傾向の指標である「代表値」とバラつきの指標である「散布度」があります。
代表値
代表値は分布の中心的傾向を表す指標で下の4つのものが用いられます。
| 代表値 | EXCEL関数 |
|---|---|
| 平均値 | AVERAGE |
| 中央値 | MEDIAN |
| 最頻値 | MODE |
| 幾何平均値 | GEOMEAN |
平均値は、測定値の総和をデータ数で割る算術平均（相加平均） です。
中央値 は測定値を全て昇順（降順）で並べて真ん中にくる数値です。データ数が奇数なら真ん中、偶数なら平均して求めます。
幾何平均（相乗平均） は測定値の積をデータ数nのn乗根です。成長率曲線や指数関数に類似した性質のデータに適しています。
代表値の特徴として正規分布ならば平均値、中央値、最頻値は等しくなります。非正規分布ならば平均値、中央値、最頻値は異なります。
散布度
分布のバラつきを表す指標を散布度といい、代表値の信頼度を示します。一部エクセルでは直接計算できないものもありますが、なるべく対応できるにまとめました。
| 代表値 | EXCEL関数 |
|---|---|
| 範囲 | MAX – MIN |
| 四分位数 | QUARTILE |
| 四分位偏差 | (Q3-Q1)/2 |
| 分散 | VAR |
| 標準偏差 | STDEV |
| 変動係数 | AVERAGE/STDEV |
範囲は最大値と最小値の差です。
四分位数 は測定値全てを昇順（降順）に並べ、4等分したものです。QUARTILE関数は[配列, 戻り値]を入力して使用します。配列はデータ範囲であり、戻り値は0が最小値、1が第1四分位数(Q1,25%)、2が第2四分位数（Q2,中央値と等しい）、3が第3四分位数(Q3,75%)、4が最大値です。
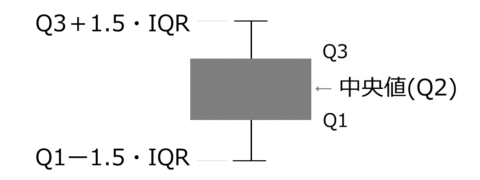
Q3-Q1のことを四分位範囲（interquartile range, IQR）と呼び、四分位範囲を2で割ったのが四分位偏差です。
分散 は（母平均－測定値）2をデータ数で割ったものであり、標準偏差 は分散の平方根です。
3つの代表値、平均値・中央値・最頻値の使い分け
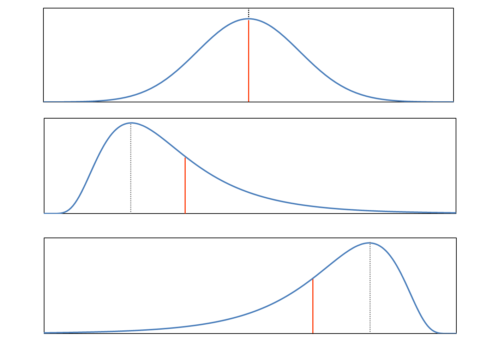
よく実験など測定値から平均値、標準偏差を求めることがあります。しかし、代表値を適切に設定しないと結果をきちんと把握できていない状況になってしまうので注意が必要です。異なるパターンの分布で実例をみてみましょう。
平均値は赤線の位置で点線は最頻値です。中央値は平均値と最頻値の間になります。対称性のある分布では平均値は中心的傾向を反映しますが、偏りがある場合平均値は不適切になります。つまり分布形状により平均値を使っても分布の特徴を表す指標にならないことがあります。
余談ですが、左に凸の分布（2個目のグラフ）は国民所得の関係でよく話題となります。国民生活基礎調査から平均所得は546万円ですが、約60%の人は平均値より低く中央値は428万円、さらに最頻値は300万円台となります。自分が取り扱うデータをグラフでみて、何を代表値として表現するのかが大事です。
論文でよく使われる代表値・散布度の表記
学術論文で論文基本統計量を使って記述される表現法を紹介します。
- 平均値±標準偏差 （min ー MAX）
- 幾何学的平均値 （25% ー 75%値）
平均値は標準偏差の組み合わせはこれは正規分布を過程する場合の表現を意味します。
解析するデータ分布が正規分布以外の場合は下の幾何学的平均値を使って表現をします。
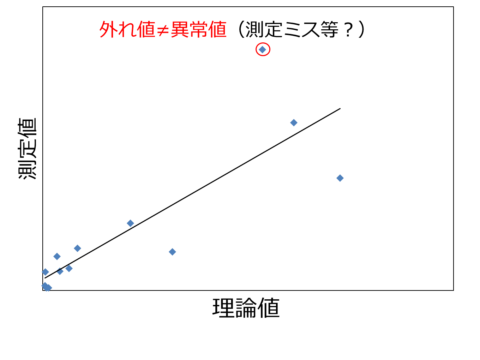
外れ値（≠異常値！）
外れ値は統計において他の値から大きく外れた値です。データ解析をしていると外れ値の存在を考慮すべき場面に出くわすことがあります。外れ値は統計において他の値から大きく外れた値であり、異常値とは表現しません。
測定ミスなど人為的でない場合は解析に含めるか慎重に考えていく必要があります。
外れ値の表現方法
よく外れ値を表現する方法として標準偏差σを用いる場合、四分位範囲IQRを用いる場合があります。
- σを用いた外れ値
- IQR (interquartile range)を用いた外れ値
正規分布を仮定
1σ：68.26%, 2σ：95.44%, 3σ：99.74%
正規分布において、平均値から±2σ離れた点までの確率が95.44%です。
標準正規分布で1.96σがちょうど95%になります。しかし通常はキリが良い2σを基準に設定することが多いです。
IQRを用いた表現は箱ひげ図とも呼ばれます。
Q1～3までのＱは散布度の四方位数です。
これらの表現は論文のグラフでよく見かけられます。
まとめ
グラフ化することでデータの傾向を捉えることができ、どうやって表現すべきなのか決定できます。データ数の大きさによらず、習慣的にデータを可視化することをお勧めします。
測定精度が妥当なのか外れ値を考慮することは大切です。多くの場合、まずヒストグラムを描き傾向を見るのが最速のアプローチになります。
