統計学は研究や教育分野だけでなくビジネスでも注目されています。しかし統計って親しみにくく理解しにくい方も多いと思います。ふだん大学で学生たちに講義していますが、知識をより共有するためもここでまとめておきます。
研究発表や論文執筆はもちろん、日々の成果を他の人へプレゼンするときにデータについて統計的手法による処理結果を与えることで内容に客観性を持たせることが期待できます。
はじめに統計の一般に関係するいくつかのポイントを整理しましょう。
統計とは
正しい測定条件のもとで測定したデータを集計し、グラフに表現するなどして規則や法則性を見出し、その正当性を検証する方法論です。単に集団から平均値や標準偏差を算出することも、統計解析の一歩と言えます。
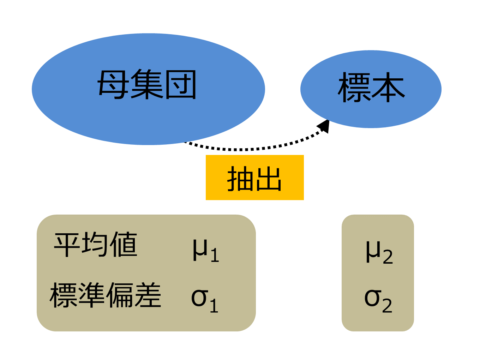
研究において、全数調査(母集団のすべてのデータをとること)は現実的に不可能な場合が多いです。限られたパズルのピースから全体像を予測するように、多くの研究では一部の標本を使って、母集団の特性を予測していくこととなります。
データ分析法(記述統計、推計統計)
データ分析は分析の過程から記述統計と推計統計の2つに分類されます。推計統計ではさらに、推定と検定という過程に分類されます。
記述統計
母集団から抽出した標本の数値を元に、母集団の特性を簡約して表現することです。
平均値は要約統計量の数値、表やグラフなどを用いてデータの特徴や傾向を捉えるために行います。
推計統計
一部の標本から全体(母集団)の特徴、性質を推測します。推定は点推定と区間推定があり、検定には仮説検定があります。
- 全体の平均値はどこにあるのか
- 信頼区間〇%(通常95%)
検定の例
- 全体の平均値が想定した値と違うのか
- 2つの群で平均値に差はあるのか
点推定
母集団から抽出した標本統計量を算出し、それを未知の母集団の推定値として用います。言い換えれば、平均値や標準偏差などある1点の情報をそのまま使用して母集団を推定します。しかし、標本を抽出する動作は誤差を伴うため通常は点推定でなく区間推定を用います。
区間推定
求めたいパラメータ値(たとえば母集団の平均値)を推定するために標本から母平均の存在する確率が(1-α)以上になる区間を求め保証します。αは真値(母平均)が求めた区間に入らない確率であり、有意水準と呼びます。棄却域に相当する確率でもあり危険率(critical rate)とも言います。1-αは信頼係数であり、簡単に言ってしまえば求めた区間に入る確率に対応します。1-α=0.9なら90%信頼区間、1-α=0.95なら95%信頼区間となります。
仮説検定
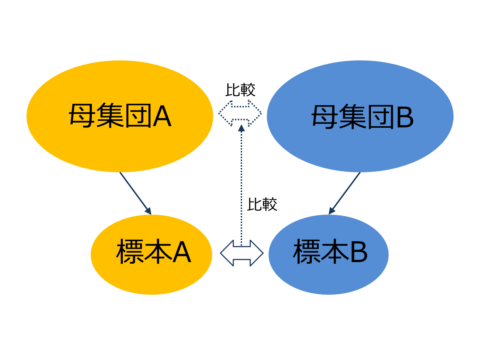
仮説検定は、異なる母集団から抽出された標本A、Bに対して比較をし、その結果からそれぞれの標本に対応する母集団間で差があるかどうかを検定します。つまり、2つ以上の標本から、母集団たちの関係を説明するときに使います。
たとえば、従来から新生児の平均体重が3,000gであったとします。ある年の新生児30例の平均体重が3,100gであったとき、直ちに「この年の新生児の体重は、従来より重い」と結論を出せるでしょうか?「偶然、重い新生児ばかり測定していたかもしれない」という抽出誤差の問題があります。
「この年の新生児の体重は、従来より重い」と結論を述べるには、観測された差(100g)が新生児の体重分布と比べて「意味のある差」なのか、統計的に検証する必要があります。この問題を解決するのが統計的仮説検定です。
仮説検定の手順
まず仮説H0と対立仮説H1を立てます。
「H1:今年の新生児の平均体重は従来より重い。」
母集団からn個の標本(x1,x2,…,xn)を抽出して、検定統計量T(x1,x2,…,xn )を計算します。簡単にいえば得られた標本から検定統計量Tを算出します。
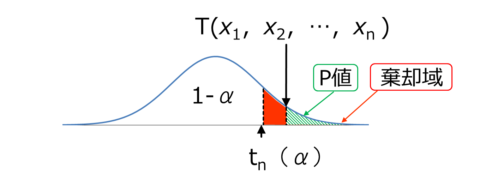
T分布のグラフは統計解析をおこなう上で頭の中でイメージすることが多いです。求めた統計検定量TがT分布のどこなのかをみて評価します。
T分布は抽出した標本を元に戻すという条件で、この処理を無限回繰り返すことで得られる分布(確率密度関数)です。
tn(α)より、外側を棄却域と呼びます。検定統計量Tが棄却域に入る場合は、有意水準αでH1を棄却し、H0を採択します。
P値はT分布において、検定統計量Tより外側(右側)の面積が全分布面積に対する割合(比)を表します。
続いて検定統計量TからP値を求めます。P値はH0が正しいのにも関わらず誤って棄却してしまう確率です。つまりこの例では差が無い確率です。P値が小さいほど小さな危険率で対立仮説が成立することを意味します。
最後に得られたP値をもとに判定します。よく論文などで使用される有意水準に0.05というものがあります。P値が0.05より大きされば仮説H0を棄却できない、つまり統計的な差は無いと言えます。逆にP値が0.05より小さい場合、対立仮説H1を採用し、統計的に差があると言えます。
- P>0.05(0.01)
- H0を棄却できない
- P<0.05(0.01)
- H0を棄却し、H1を採用(統計的に差がある。)
まとめ
一部の標本から全体像を想像するためには推計統計が用いられます。推定は点もしくは区間で行い、検定で差があるのかないのかを確認します。P値や有意水準について解説をしました。大切な概念になりますので検定の手順(p値から仮説H0を採用するのか、対立仮説H1を採用するのか)は押さえておきましょう。