研究でデータ分析をする目的の1つに、測定したデータ間に有意差があるか調べることがあります。研究発表、論文を書く経験が少ない場合、どのように統計を使ったらいいのか判断に迷うかもしれません。
これから論文をはじめて書いたり、研究の入門として、よく使われる統計手法をまとめてみました。医学分野は、統計を学問として理解するというより、さらに実践的に使うこと多いのです。
パラメトリック検定とノンパラメトリック検定
統計で使うデータ(変数)の種類
統計で扱うデータにはさまざまな種類のものがあります。大きくは質的データと量的データに分かれます。質的データは性別「男,女」やアンケートの満足度「満足した,普通,不満だった」など、それ自体は分類(カテゴリー)で定性的な性質を示します。統計で処理する場合、これらのデータを名義的に数値化をし前者は「1,2」、後者は「1,2,3」と対応させます。一方、量的データはテストの点数、体重など数や量を示すものです。
質的データの名義尺度・順序尺度と量的データの間隔尺度・比例尺度
あらゆるデータとして数値の意味する性質を尺度(変数と呼ぶこともある)と呼びます。定性的である質的データは、名義尺度と順序尺度に分類されます。定量的うである量的データは間隔尺度と比例尺度に分類されます。
| 尺度の種類 | 例 |
|---|---|
| 名義尺度 (カテゴリカル尺度) | 名称、種類など |
| 順序尺度 | 順位、病期 |
| 間隔尺度 | 温度、テスト |
| 比例尺度 | 身長、体重、時間 |
名義尺度
単に同質・異質を決定するために名目的・名義的に名前を付けただけの特性。
順序尺度
大小関係のみ存在し、単に順序をつけただけの特性。
病期やn段階スコア(満足度)など、和や差の値に絶対的な意味を持たない。
中央値で評価できる(平均はNG)。
間隔尺度
大小関係が意味を持ち、かつ数値間の間隔(距離)が等しい特性。
和や差に意味がある。
比率は意味を持たない。(例えば10℃と20℃→2倍としない)
比例尺度
間隔尺度の性質に、絶対的な原点を加え持つ特性。
原点に意味を持つ。
身長や血圧など実際に測定した値など数量的データである「間隔尺度」と「比例尺度」の2つは統計的に同様に扱うので、間隔尺度か比例尺度か神経質になる必要はありません。
パラメトリックとノンパラメトリック
身長や水量などの量的変数(間隔尺度と比例尺度)でその分布が正規性をもつ場合、平均値や分散などのパラメータ(parameter)が意味を持ちます。このようなパラメータを用いた統計学をパラメトリック統計学(parametric statistics)と呼びます。一方、性別(男1,女2)や病期の程度(1,2,3)などの質的変数(名義尺度と順序尺度)では、その平均値が意味をもたず、異なるカテゴリーに属する人や者の数で構成され、これらのデータ処理にはノンパラメトリック統計学(nonparametric statistics)が使われます。
パラメトリックとノンパラメトリックの検定を以下にまとめておきます。
パラメトリック統計
解析するデータが2群なのか、3群以上かどうかで分かれます。
| 2群定 | ||
|---|---|---|
| 対応なし | 対応あり | |
| F検定 | 対応のあるt検定 (t検定: 1対の標本による平均の検定) | |
| p>0.05(0.01) スチューデントのt検定 (t検定: 等分散を仮定した2標本による検定) | p<0.05(0.01) ウェルチのt検定 (t検定: 分散が等しくないと仮定した2標本による検定 ) | |
| 3群以上 |
|---|
| 対応なし/対応あり |
| 一元配置分散分析 二元配置分散分析 多元配置分散分析 |
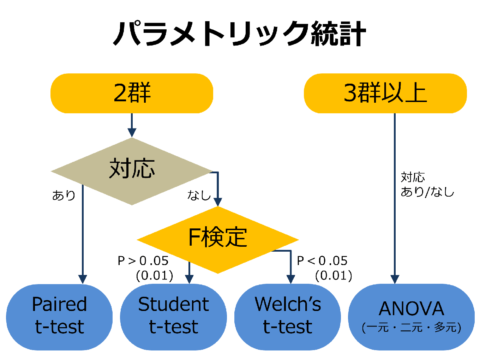
2群のデータの関係に対応がある場合、対応のあるt検定(Paired t-test)を行います。対応なしの場合、F検定を行います。その結果によってスチューデントのt検定(Student t-test)を行うかウェルチのt検定(Welch’s t-test)を行うか決めます。
3群以上では上記検定を行い、有意差があればどのデータ群で差があるのか比較します(多重比較)。分散分析で分かるのははあくまで同じかそうでないかまでです。どの水準によるものかを調べるために多重比較をします。
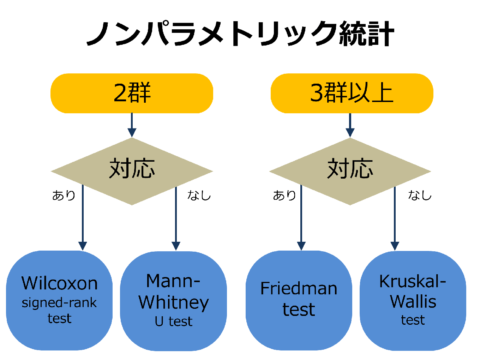
ノンパラメトリック統計
ノンパラメトリック統計には、χ2検定(chi-square test)や符号検定、符号付き順位和検定(Wilcoxon検定)、順位相関検定、Mann-Whitney検定などがあります。
| 2群 | |
|---|---|
| 対応なし | 対応あり |
| マン・ホイットニーのU検定 | ウィルコクソンの符号付き順位検定 |
| 3群以上 | |
|---|---|
| 対応なし | 対応あり |
| クラスカルウォリス検定 | フリードマン検定 |
3群以上では上記検定を行い、有意差があればどのデータ群で差があるのか比較します(多重比較)。
もし、分散が等しくなければWeltchの検定やブルンナー・ムンツェル検定を適用します。
2値データの場合
0/1などの2値データの場合、2群ならマクネマー検定、3群ならコクランのQ検定を用います。マクネマー検定やコクランのQ検定は対応ありのデータを扱います。
対応なしの場合、クロス集計表を用いてχ2検定を用います。
まとめ
最後に、おおまかに理解できるように図にまとめました。
ANOVA(analysis of variance)は分散分析のことです。一元・二元・多元はデータに合わせて1つを選びます。
アンケート調査でよく使われるノンパラメトリック統計は、省略してます。
これから研究へ取り組む多くの方に、少しでも役立てば幸いです。

コメント
群間比較をするにあたり、代表値の選択に悩んでいるところ拝見させて頂きました。
とても分かりやすく、理解をすることができたのですが、わからないことがありましたのでご質問させていただきます。
今回、学会で発表した際に平均値を用いて2群を分けたのですが、本件で平均値を用いて2群を抽出するのは妥当性に欠けますと言われました。私自身、統計学に詳しくはないため返答することが出来ませんでした。
代表値として、平均値・中央値・最頻値がありますがどのように使い分ければよいのでしょうか。正規性があるかどうかで決めるのでしょうか。なにか規則などがあれば教えて頂きたいです。
わかりにくくてすみません。
>tsuchiyaさん
コメントありがとうございます。
質問に対しての答えですが、元データは平均値ということなので量的データ(数値)だと仮定させていただきます。
まず、Excelのグラフを使って元データの分布を確認してみてください。
ヒストグラムで見た目に正規性があるか、箱ひげ図で外れ値があるか確認します。
分布の形状で使うべき代表値が変わります。
参考としてこちらの記事をご参照ください。
https://crossnote.jp/data-analysis_basic-statistics_outliers/
もし、正規性があれば平均値による2群間の検定を使います。t検定のWeltchを使ってください。
正規性が無い(ノンパラメトリック)ならば、マン・ホイットニーのU検定かウィルコクソンの符号付き順位検定となります。
ただし、マンホイットニーのU検定は制約(2群の確率変数の分散が等しいことを前提とする)があります。分散が等しくない場合は、Weltchの検定やブルンナー・ムンツェル検定(Brunner-Munzel test)を使ってください。
回答ありがとうございます。
元データは膝蓋骨が側方にどのくらい移動しているかを距離で表し、データとして使用していますので間隔尺度と思われます。
母集団で正規性があれば平均値を使用し、母集団が非正規性であれば中央値または最頻値を使用し2群に分けるということでしょうか。
また、参考として教えて頂いた記事には、代表値の特徴として、非正規分布でならば平均値、中央値、最頻値は異なると書かれているのですが、中央値と最頻値はさほど変化がないのではないですか。
違っていたら申し訳ございません。
>tsuchiyaさん
このデータから考えると、距離が0ならば基準から差(ズレ)が無いという意味を持つので、間隔尺度でなく比例尺度になります。
しかし、間隔と比例尺度は統計的に扱いは同じなので特に問題なしです。
さて、代表値に関しては”何を表現したいか”で変わります。全体の中心的な傾向を表すのであれば、正規性があるときに平均値を、非正規のときに中央値を示します。
ヒストグラムにおけるピークの位置を表すのであれば、正規性があるとき平均値が等しく(中央値や最頻値も数値はほぼ同じ値)、非正規のときに最頻値です。
参考記事についてですが、ヒストグラムの分布に偏りがある場合、3つの値は異なります。左に偏りがあれば、最頻値<中央値<平均値です。(「3つの代表値、平均値・中央値・最頻値の使い分け」の後半で解説しております。)
補足ですが、2群間のデータを示す方法は、正規性があれば平均値±標準偏差、非正規なら幾何平均(もしくは中央値)±四方位数の25%-75%と記載します。