データ収集をするときに、どれくらいの精度を必要とするのか事前に計画しておくことでサンプルサイズ(標本数)を決定することができます。
Contents
サンプルサイズの設計
サンプルサイズの設計について順序を説明します。まず仮説を立てて目的に対応した解析方法を選択します。次にサンプルサイズの設計に必要な情報を準備します。ここでは予備的研究や先行研究の結果を参考にして想定・過程をします。
サンプルサイズの代表的な決定法
サンプルサイズの決定法として代表的なものをいくつか紹介しておきます。必要項目を入力すれば自動計算してくれるのでとても簡単に行うことができます。
その他にも決定法はあります。
サンプルサイズの設計に必要なパラメータをまとめておきます。
| パラメータ | 手法 | 備考 |
|---|---|---|
| 母比率 | 1 |
|
| 有意水準(α) |
| |
| 両群の人数比 | ||
| 誤差 | 1,2,3 |
|
| 信頼度(1-α) | 1,2,3 | |
| 標準偏差(σ) | 2,3 |
|
| 検出力(1-β) |
パラメータの解説
特に理解しておきたいパラメータについて補足しておきます。
有意水準
よく使われる数字は5%(1%)です。これは「帰無仮説を棄却する誤りは5%以下」ということに対応します。本当は帰無仮説が正しかったにもかかわらず、それを棄却することによって誤りを犯す危険を100回のうち5回までは認めてもいいということです。有意水準はα、信頼度は1-αなので95%となります。
前項を言いましたがこれらのことから有意水準のことを危険率とも呼びます。帰無仮説が正しいのに棄却してしまうことを「第1種の過誤」、 対立仮説が正しいのにそれを検出できない「第2種の過誤 」と呼びます。
誤差と信頼度
誤差を5%、信頼度を90%としたとき、これは100回中90回は サンプル比率と母比率との差が±5%の範囲内に収まることを意味します。
誤差率とサンプルサイズ
必要な標本数は、あらかじめ十分な精度が得られるように計画して決めておくべきものです。データを収集する前に検討して研究計画書を作成します。
あらかじめ定めた誤差率(例えば1%)を達成するために必要な標本数を調査します。(※ただし、実際には期間等の制約を受けます。)
誤差率は「標準誤差÷推定値(平均値等)」と定義され、誤差率が小さいほど、推定精度が高くります。研究等でサンプルサイズの設計について、事前に研究計画書をかく場合、誤差率を考えておくとよいです。
仮に誤差率を5%、母比率を50%としたとき、有意水準5%とすると385個のデータが必要になります。また、標準偏差を10、誤差5%、有意水準5%とすると18個のデータが必要になります。(ただし、対応がない2群の場合、nは123個となる。)
仮に有意水準を5%、検出力を95%としたとき、効果量(μ1-μ2/σ平均の差が標準偏差の何倍か)の違いによって必要なサンプル数がどう変化するのかを表にまとめました。
| 効果量 | サンプル数 |
|---|---|
| 2.0 | 8 |
| 1.5 | 13 |
| 1.0 | 27 |
| 0.9 | 34 |
| 0.8 | 42 |
| 0.7 | 55 |
| 0.6 | 74 |
| 0.5 | 105 |
| 0.4 | 164 |
| 0.3 | 290 |
上記は両側で2群間の平均の差を検定する場合です。
どんな試料でも、検定を行う場合、目安20個、できれば25個以上は欲しいです。
サンプルの抽出方法と誤差
標本調査によって母集団の特性を推定するためには、必ず「無作為抽出」を行います。
標本抽出を行う場合は、母集団をいくつかの抽出単位(男、女、目的に応じて決める)に分け、全ての抽出単位が選ばれる確率が等しくなるように工夫することが重要です。
無作為抽出の方法
標本から母集団の特性を推測するためには、無作為抽出を行わなければならなりません。代表的でない(偏りのある)データから母集団の特性は推測できないからです。主な無作為抽出を表にまとめておきます。
- 単純無作為抽出法
- 層化無作為抽出法
- クラスター抽出法
- 層化クラスター抽出法…etc
単純無作為抽出は、文字通り、乱数を用いてサンプル対象を決定します。住民調査やアンケートでよく用いられます。
層化無作為抽出ではあらかじめ、対象を複数の層に分けてから無作為抽出をする方法です。たとえば、病院を病棟ごとに分け、各病棟から無作為に抽出をするといった感じです。もちろん年齢とかで分けることも可能です。
クラスター抽出では、病院全体を対象とする場合、乱数によって10病棟を選び、その10病棟の患者全員を対象として調査を行います。クラスターは日本語で集落となりますが、母集団をいくつかのクラスターに分け、クラスターを抽出単位として無作為に選び、クラスター内の全数調査をします。
では標本抽出によってどんな誤差が起こるのか、どんな偏り方があるのかを考えたいと思います。
標本抽出の誤差・偏り
統計における誤差は、真の値と観測値とのズレを意味します。標本調査ではつきものです。
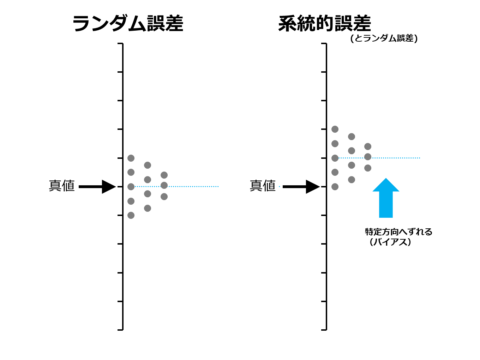
標本抽出の誤差・偏りには、ランダム誤差と系統的誤差の2つがあります。
- ランダム誤差
偶然現象によって生じたずれ。標本抽出における誤差を特に標本誤差という。統計学である程度制御可能。 - 系統的誤差
何らかの理由により、一定方向(正または負) に生じたずれ。「偏り」ともいう。統計学で制御不可能。
ランダム誤差
ランダム誤差は標本誤差とも呼ばれ、標本抽出をする段階で必ず発生します。標本数を多くすることで、ランダム誤差を小さくできます。正負方向に同様におこり、平均すると0になります。
系統的誤差
一方向に偏った結果となってしまうものです。統計学で制御不能であり、系統的誤差を標本抽出の段階で見つけるのは少し難しいです。しかし、クラスターの見直しで差があるかどうかなど、データの見方をかえることで系統的誤差を発見できることがあります。標本の抽出の仕方を見直すしかないです。
誤差を減らす工夫
標本抽出の誤差を減らす工夫としては可能な限り標本数を増やし、無作為抽出法を適切に用いることが重要です。クラスターの設定をしっかりすれば後の解析で交絡、つまりバイアスの問題をクリアすることにつながります。
- ランダム誤差:標本数を増やす。
- 系統的誤差:無作為抽出法を適切に用いる。
ex.クラスター(集落)の設定の見直し等
誤差の分類
誤差はタイミングや性質によって分類されます。誤差がタイミングにより「標本誤差」と「測定誤差」に分かれます。標本誤差は
標本抽出の段階で生じる誤差であり(これまでの話)、測定誤差は測定する(データ収集)ときに起こる誤差です。
- どのタイミングで起こるのかによる分類
- 標本誤差(今までの話)
- 測定誤差
- 性質による分類
- 系統的誤差(偏り)
- ランダム誤差(平均すると0)
測定誤差も、性質からランダム誤差と系統的誤差に分類されます。ランダム誤差は真の値に対して特定の方向に偏らず測定値が両側にバラつくのに対して、系統的誤差は真の値からある特定の方向にずれます。
測定のランダム誤差と系統的誤差
測定誤差についてランダム誤差と系統的誤差の要因として具体的な例をみてみましょう。ランダム誤差は、「日間変動や日内変動」があります。被測定者のその日、その時々の体調の変化が考えられます。複数回測定すれば、その平均が真の値に近づけれます。
一方系統誤差は「被験者の測定条件」や「被験者、測定者、測定機器の“くせ”」があります。測定条件はある特定の気候や季節に行ったことで生じます。また対象となる被験者がウソの申告をする可能性や、測定者の性格でコード配置が不統一であったり、測定機器が絶対量を出さないときには注意が必要です。
データ収集のためにはランダム誤差や系統的誤差を小さくできるように気をつけてみてください。
まとめ
データ数は多くとれれば統計的に堅牢な結果が得られますが、どのくらいデータ数が必要なのか計画することでその後の計画が立てやすくなります。結果を出すとき、確証のある数字を使えるように設計しましょう。